classification 결과를 평가해봅시다.

3 분 소요

classifier의 성능을 어떻게 평가할까요?

y_true, y_pred 가 각각 있습니다. 이를 활용해서 현재 분류된 결과의 성능을 어떻게 잘 평가할 수 있을까요?
보통 classification을 평가하는 metric들은 binary classification을 기준으로 만들어져 있습니다.

confusion matrix

맨날 헷갈리는 그것!, 우선 그림을 봅시다.

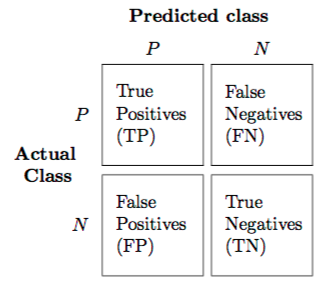
binary classification은 Positive/Negative를 예측하는 건데, 이는 총 4 가지 상황으로 분류될 수 있죠. 쓰고 나면 명확한데 항상 헷갈립니다. 진짜 진짜 많이 봤는데 매번 헷갈려요ㅠㅠㅠ
- True(진짜) Positive(양성): 양성으로 예측했고, 그게 맞다
- True(진짜) Negative(음성): 음성으로 예측했고, 그게 맞다
- False(가짜) Positive(양성): 양성으로 예측했고, 그게 틀리다(사실 음성)
- False(가짜) Negative(음성): 음성으로 예측했고, 그게 틀리다(사실 양성)
각각, TP, TN, FP, FN 이라고 불리고, metric을 계산할 때, 이 confusion matrix를 활용합니다.
Confusion matrix가 헷갈리는 이유는 (제 생각에) Positive/Negative 구분이 애매하기 때문입니다. binary classification 의 경우에 그냥 class 0으로 분류되거나, class 1로 분류되거나 일 뿐이지, 굳이 positive/negative 로 명명되는 이유가 있느냐? 는 것이죠.
그래서 조금 더 이해하기 쉬우려면, 이 분류가 병을 진단하기 위해 사용되었으며, 따라서 TP + FN, Actually 양성인 집단의 수가 적다, 라고 생각하면 좀 더 이해하기 쉽습니다.

accuracy(정확도)

(양성이든 음성이든 상관없이) 예측한 것들 중에서 얼마나 맞추었는가?
- 이게 매우 기본적인 지표이긴 한데, 실제 양성인 경우(TP+FN)가 너무 작을때(실제로 병에 걸린 사람은 적으니까)는 문제가 될 수 있습니다.
- 만약 1%가 양성이고, 1%가 음성이면 “모두 양성으로 진단하는 멍청한 분류기”도 99%의 accuracy를 가지게 되거든요.

\[{tp + tn} \over {tp + tn + fp + fn}\]

precision and recall

precision

양성으로 예측한 놈들 중에서, 실제로 양성인 놈이 얼마나 있는가?
- 병원에서 나한테 ‘님 양성’이라고 하면, 아주 슬플 것 같아요. 그런데, 그게 틀릴 수도 있잖아요, 사실? 이것은 내가 너님을 양성이라고 했을때, 그 판단이 틀릴 확률을 말합니다.
- 이 값이 높을수록 의사의 진단이 의미가 있는 것이죠.

\[{tp} \over {tp + fp}\]

recall(검출력)

실제로 양성인 놈들을, 얼마나 예측해냈는가?
- accuracy의 한계는, 양성이 1%일 때는 항상 negative라고 하는 분류기조차 99%의 값을 가진다는 것입니다.
- 따라서, recall은 이 한계를 극복하기 위해서, actual class 중에서 얼마나 잘 걸러냈는가를 평가합니다.
recall 은 sensitivity 라고 말해지기도 합니다.

\[{tp} \over {tp + tn}\]

precision 과 recall간에는 어느 정도 트레이드오프가 발생합니다.
- 상황1: 예를 들어서, recall 을 올리기 위해서, 웬만하면 positive라고 한다고 합시다. 의사가 모든 사람한테 “당신은 병에 걸렸습니다”라고 하면, recall은 1이 되지만, precision은 매우 낮아지겠죠.
- 상황2: 예를 들어서, precision을 올리기 위해서 웬만하면 negative라고 한다고 합시다. 의사가 정말 확실할 때만 “당신은 병에 걸렸습니다”라고 한다면, precision읖 높아지지만, recall은 매우 낮아질 것입니다.

F1-score

즉, precision, recall 모두 매우 중요한데, 이 밸런스를 평가하기 위해서 F1-score를 사용합니다.

\[F1 = { Precision * Recall } \over { Precision + Recall }\]

ROC(Receiver operating characteristic) curve

sensitivity와 specitivity가 각각 서로 어떻게 변하는지를 2차원 평면 상에 표시한 것이 ROC curve가 된다. 이 두 값이 모두 높게 유지되어야 좋은 분류기라고 할 수 있다.
따라서, 이전의 값들은 y_pred, y_true만 넘겨줘도 괜찮았는데, ROC curve부터는 y_pred_proba도 함께 넘겨주는 것이 필요하다. 그래야, clf_threshold를 움직이면서, sensitivity와 specitivity 간의 트레이드오프를 계산할 수 있음.

sensitivity

recall과 같은 의미.
병에 걸린 사람을 병에 걸렸다고 얼마나 잘 분류해냈는가?

\[{tp} \over {tp + tn}\]

specitivity

건강한 사람을 건강하다고, 얼마나 잘 분류해냈는가?

\[specitivity = {tn} \over {tn + fp}\]

AUC(Area Under Curve)

ROC curve 의 아래 면적을 계산한 값

do it!

sklearn에서 metric들을 계산하고 그림도 그려봅니다.

import numpy as np 
import matplotlib.pyplot as plt 

from sklearn.metrics import accuracy_score, precision_score, precision_recall_curve
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import roc_curve, roc_auc_score

from sklearn.linear_model import LogisticRegression

def learn_and_eval_clf(x, y_true):
    clf = LogisticRegression(random_state=42)
    clf.fit(x, y_true)

    y_pred = clf.predict(x)
    print("accuracy_score: {}".format( accuracy_score(y_true, y_pred)))
    print("precision_score: {}".format( precision_score(y_true, y_pred)))
    print("AUC: Area Under Curve: {}".format(roc_auc_score(y_true, y_pred_proba[:, 1])))
    #print("Classificcation Report: \n{}".format(classification_report(y_true, y_pred)))
    #print("Confusition matrix: \n{}".format(confusion_matrix(y_true, y_pred)))

    y_score = clf.decision_function(x)
    precision, recall, _ = precision_recall_curve(y_true, y_score)
    fpr, tpr, _ = roc_curve(y_true, y_score)

    f, axes = plt.subplots(1, 2, sharex=True, sharey=True)
    f.set_size_inches((8, 4)) 
    axes[0].fill_between(recall, precision, step='post', alpha=0.2, color='b')
    axes[0].set_title('Recall-Precision Curve')

    axes[1].plot(fpr, tpr)
    axes[1].plot([0, 1], [0, 1], linestyle='--')
    axes[1].set_title('ROC curve')
    #plt.save
    return f

"""
- 임의로 각각 평균이 0.0, 0.25인, 큰 차이가 나지 않는 샘플들을 뽑아서, 분류해본다. 
"""
sample_size = 100
x = np.vstack(
    [np.random.normal(0, 1, sample_size*2).reshape(sample_size, 2), 
     np.random.normal(0.25, 1, sample_size*2).reshape(sample_size, 2), 
    ]
)
y_true = np.array([0 for i in range(0, sample_size)]+[1 for i in range(0, sample_size)])


try1 = learn_and_eval_clf(x, y_true)
try1.savefig('../../assets/images/markdown_img/20180530-recall_Precision_curve_roccurve_1.svg')
"""
- 임의로 각각 평균이 0.0, 2인, 큰 차이가 나지 않는 샘플들을 뽑아서, 분류해본다. 
"""
sample_size = 100
x = np.vstack(
    [np.random.normal(0, 1, sample_size*2).reshape(sample_size, 2), 
     np.random.normal(2, 1, sample_size*2).reshape(sample_size, 2), 
    ]
)
y_true = np.array([0 for i in range(0, sample_size)]+[1 for i in range(0, sample_size)])
try2 = learn_and_eval_clf(x, y_true)
try2.savefig('../../assets/images/markdown_img/20180530-recall_Precision_curve_roccurve_2.svg')

당연하지만, 평균간의 거리가 멀수록, 데이터 간의 차이가 명확하고, 분류기가 더 잘 학습할 수 있다.

accuracy_score: 0.585
precision_score: 0.5825242718446602
AUC: Area Under Curve: 0.8396
accuracy_score: 0.935
precision_score: 0.9223300970873787
AUC: Area Under Curve: 0.8396

wrap-up

현재로서는 binary classification에 대해서 적용했음.
그냥 accuracy를 체크해야, 대략적으로 얼마나 정확한지 알수 있고, roc_auc_score도 확인하여, 맞는 경우, 아닌 경우에 tradeoff가 적도록 잘 분류하는 분류기인지를 평가하고
confusion_matrix를 통해 문제가 되는 부분이 없는지 한번 파악해본다.

Twitter Facebook LinkedIn

frhyme