distance를 비교해봅시다.

비슷한가 안 비슷한가!

• 데이터 분석을 하거나 해야할 때, 많이 쓰이는 measure 중 하나는 similarity(distance)라고 할 수 있습니다. 이 아이들은 비슷한가? 비슷하면 얼마나 비슷한가? 는 항상 직관적으로 궁금해지는 부분입니다.
  • similarity와 distance는 서로 역수의 관계라고 생각하셔도 무방할 것 같은데요, similarity의 경우는 range(0,1)라고 생각하면 됩니다. 완전히 같으면 1을 완전히 다르면 0을 가진다고 보면 됩니다. 약간 회귀분석(regression)에서 r-square와 비슷한 느낌이라고 생각하시면 될것 같습니다.
  • distance는 사실 range가 따로 있지는 않습니다. 따라서 sample이 n개 가 있다면, n(n-1)/2 의 거리에 대해서 표준화를 진행하는 것이 필요합니다. 그냥 간단하게는 minmaxscaling을 해도 되는데, 이렇게만 해도 될까요? 흐음, 좀 크리어하지는 않군요.
• 아무튼 예를 들어서 clustering을 해야 할때, 이 아이들의 거리는 어느 정도 떨어져 있다고 생각해야하나? 그 거리를 측정하는 방식에 따라서 cluster 들의 구성은 달라지게 됩니다.
• 우리가 고등학교 수학때 배운 일반적인 distance 측정은 euclidean방식입니다. 여전히 이게 많이 쓰이고 있기는 하지만, 다른 distance과의 차이점들이 있죠.

Euclidean distance

• 두 점간의 직선거리를 측정하는 일반적인 방법입니다.

formula

\[\sqrt{\sum_{i=0}^k (x_i - y_i)^2}\]

code

from math import *

def euclidean_distance(x,y):
    return sqrt(sum(pow(a-b,2) for a, b in zip(x, y)))

Mahalanobis distance

• 기존의 유클리디안 거리의 경우는 확률분포를 고려하지 않는다라는 한계를 가진다. 거리상으로는 가깝다고 해도 실제로는 잘 등장하지 않는 샘플의 경우 생각보다 더 멀리 있을 수 있다. 따라서 확룰 분포를 고려하여 계산하는 방법이다.
• 간단하게는 공분산을 고려하여 거리를 잰다고 생각하면 된다.
• 아래 그림에서, 위쪽 별을 A라고 하고, 오른쪽 별을 B라고 하고 [0, 0]부터의 거리를 계산해보면 B는 유클리디안 거리 상에서 더 멀리 있지만, 분포를 고려하면 오히려 가까이 있다는 생각이 들 수 있다 이러한 것을 Mahalanobis distance라고 한다.
• 물론 이 거리를 측정하기 위해서는 단지 x, y 두 점만 필요한 것이 아니고 covariance matrix 가 필요하다.

• scipy의 코드scipy.spatial.distance.mahalanobis를 그대로 사용한다.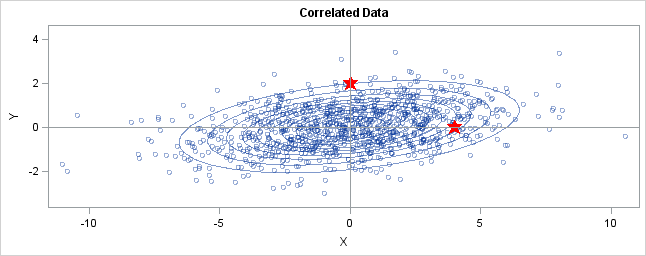

  

Manhattan distance

• manhattan distance의 경우는 직선거리가 아닌 차원별 차이를 따로 측정해서 그 합을 계산한다고 보면 된다. 막힌 곳이 없는 평지에서는 euclidean distance가 의미가 있지만, manhattan처럼 건물이 많은 곳에서는 직선거리가 아닌 가로와 세로의 각각의 합이 더 정확한 거리를 의미할 수 있다.

formula

\[\sum_{i=0}^k |x_i - y_i|\]

code

def manhattan_distance(x,y): 
    if len(x)==len(y):
        r = 0 
        for i in range(0, len(x)):
            r+=abs(x[i]-y[i])
        return r
    else:
        return "error"

Minkowski distance

• generalized form of Euclidean distance and manhattan distance
• 앞서 말한 euclidean distance와 manhattan distance의 일반적인 방법입니다.
  • \(\lambda = 1\) : manhattan dist.
  • \(\lambda = 2\) : euclidean dist.
  • \(\lambda = \infty\) : Chebyshev dist.

formula

\[d^{MKD}(x, y) = ({\sum_{k=0}^{n-1} {| x_k - y_k |}^\lambda })^{1/\lambda}\]

• 여기서 중요한 것은 마지막, Chebyshev distance가 헷갈릴 수 있다. 이 거리는 보통 king's distance라고 해도 상관없는데, 체스에서 왕의 경우는 대각선으로도 갈 수 있고, 직선으로 움직일 수 있다.
• 예를 들어, 체스판 왼쪽 위를 [0,0] 으로 두었을 때 [3,3]까지 가는데 필요한 움직임은 3이고, [3,0]으로 가는데 필요한 움직읻 또한 3이다. 이를 측정할 수 있는 거리가 chebyshev distance이다.
• 그래서 이게 언제 유용한데요? 언제 쓰면 되는데요? 라고 물어본다면 음…..글쎄….요….

code

def minkowski_distance(x, y, lam):
    r = 0
    for a, b in zip(x, y):
        r+=(abs(a-b))**lam
    return (r)**(1.0/lam)
print(minkowski_distance([3,3], [0,0], 500))
print(minkowski_distance([3,4], [0,0], 500))
print(minkowski_distance([3,0], [0,0], 500))

3.0041617671340037
4.0
3.0

cosine distance

• 이는 두 벡터간의 실질적인 좌표간의 거리보다는 angle 차이를 본다. 만약 이 두 벡터가 orthogonal하다면 이 측정값은 0이 되고, 같은 방향을 가리킨다면 1이 된다. 반대로 반대 방향을 가리킨다면 -1이 된다.

formula

\[A \cdot B \over ||A|| \ ||B||\]

code

def cosine_similarity(x,y):    
    def square_rooted(x):
        return sqrt(sum([a*a for a in x]))
    numerator = sum(a*b for a,b in zip(x,y))
    denominator = square_rooted(x)*square_rooted(y)
    return round(numerator/denominator, 2)

jaccard distance

• jaccard distance의 경우는 서로 다른 fininite 한 set에 대해서 사용될 수 있다. 서로 다른 두 object가 만들 수 있는 union의 개수 대비 intersection이 얼마나 있는지를 사용해 그 유사도를 측정한다.
• 이전의 distance들이 numeric vector 를 대상으로 했다면, 이 distance의 경우는 boolean vector를 대상으로 한다고 할 수 있다.

code

def jaccard_similarity(x,y):
    intersection = set(x).intersection(set(y))
    union = set(x).union(set(y))
    return len(intersection)/len(union)

reference

• http://dataaspirant.com/2015/04/11/five-most-popular-similarity-measures-implementation-in-python/
• https://docs.scipy.org/doc/scipy/reference/spatial.distance.html