python에서 수를 다루는 방식.

python에서 숫자를 정확하게 다룹시다

• pyconkr2017에서 발표되었던 보다 정확한 숫자 계산이라는 발표의 내용을 정리해 봤습니다. 특히 해당 발표의 발표자분은 8퍼센트의 CTO이십니다. 숫자를 잘 다루어야 하는, 특히 소수점 단위까지 매우 정확하게 다루어야 하는, 금융업무를 하시는 분이 이 발표를 하셨던 것은 어쩌면 너무 당연한 이야기겠죠.

half rounding in python(default)

• python 3.0 부터는 rounding 방법이 바뀌었습니다. 이를 banker’s rounding이라고도 한다는데, 다음처럼 반올림이 됩니다.
  • round(3.5) ==> 4
  • round(4.5) ==> 4
• 이번에 처음 알게 된 사실인데, 반올림을 하는 방법도 여러 가지가 있고, 그 방법에 대한 상세한 가이드라인이 IEEE754에 작성되어 있습니다. 아래는 그 내용이 담겨있는 테이블이구요.

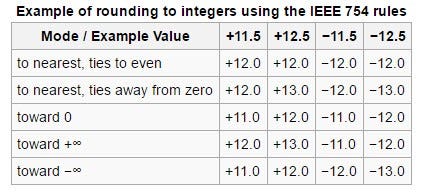
• python의 경우 3.0부터 default값이 변경되었고, What’s new in python 3.0을 보시면 다음 내용이 작성되어 있습니다.

The round() function rounding strategy and return type have changed. Exact halfway cases are now rounded to the nearest even result instead of away from zero. (For example, round(2.5) now returns 2 rather than 3.)

• 혹시나, numpy를 쓰면 다를거야!, 라고 생각하시는 분들이 있을텐데 달라지지 않습니다.

## numpy를 쓴다고 해서 rounding 방법이 달라지지 않습니다. 
import numpy as np 
str_lst = ['round(3.5)', 'round(4.5)',
           "np.round(3.5)", 'np.round(4.5)']
for s in str_lst:
    print(f"{s} ==> {eval(s)}")

round(3.5) ==> 4
round(4.5) ==> 4
np.round(3.5) ==> 4.0
np.round(4.5) ==> 4.0

• 그렇다면, 왜 학교에서 배운 방식대로 반올림을 하는 것이 아니라, banker’s rounding을 쓰는 것일까요?
• 아래 코드를 봅시다.

xs = [1.5 + i for i in range(0, 10)]

str_lst = ['sum(xs)', ## 그냥 더하는 경우 
           'sum(round(x) for x in xs)', ## banker's rounding으로 계산해서 더하는 경우 
           'sum(round(x+0.0000001) for x in xs)', ## 우리가 보통 하는 방식으로 반올림해서 더하는 경우 
          ]
for s in str_lst:
    print(f"{s} ==> {eval(s)}")

• banker’s rounding이 아닌 우리가 통상적으로 알고 있던 계산 방법으로 반올림을 할 경우, 나중에 값을 다 합치거나 하는 연산을 했을 때 오차가 커지는 일이 발생할 수 있습니다. banker’s rounding은 이를 방지하기 위한 방법인 셈이죠.

sum(xs) ==> 60.0
sum(round(x) for x in xs) ==> 60
sum(round(x+0.0000001) for x in xs) ==> 65

rounding float(below 0)

• 0보다 작은 소수들에 대해서 반올림을 수행한다고 해봅시다. 아래 코드를 수행해봅니다.

for x in [0.25, 0.35, 0.45, 0.55, 0.65, 0.75]:
    print(f"{x} ==> {round(x, 1)}")

0.25 ==> 0.2
0.35 ==> 0.3
0.45 ==> 0.5
0.55 ==> 0.6
0.65 ==> 0.7
0.75 ==> 0.8

• …?? 뭔가 이상하지 않나요? 0.35를 반올림했더니, 0.3이 나왔습니다. banker’s rounding에 맞게 나오려면 0.35는 0.4로 rounding되는 것이 타당하죠.
• 값을 꼼꼼히 봅시다. 0.0625, 0.125, 0.25, 0.75와 같이 2의 exp형태로 표현되는 경우는 오차가 없이 값이 똑 떨어지는 반면, 다른 값들의 경우는 정확히 그 값이 들어있는 것이 아니라, 근사값이 들어가 있습니다. 특히 0.35의 경우는 0.349의 값이 들어있고, 따라서 반올림하면 0.3이 되는것이죠.

import decimal 
for x in [0.0625, 0.125, 0.25, 0.35, 0.45, 0.55, 0.65, 0.75]:
    print(f"{x} ==> {decimal.Decimal(x)}")

0.0625 ==> 0.0625
0.125 ==> 0.125
0.25 ==> 0.25
0.35 ==> 0.34999999999999997779553950749686919152736663818359375
0.45 ==> 0.450000000000000011102230246251565404236316680908203125
0.55 ==> 0.5500000000000000444089209850062616169452667236328125
0.65 ==> 0.65000000000000002220446049250313080847263336181640625
0.75 ==> 0.75

• IEEE754 표준에 의한 값을 저장하는 방식을 보면, 다음과 같습니다. 즉 값을 그대로 저장하는 것이 아니라 (sign) * fraction * 2 ^ exponent와 같은 방식으로 저장하는 것이죠.
• 따라서 2의 값으로 표현될 수 있는 경우에는 값이 정확하게 똑 떨어지는 반면 그렇지 않을때는 위처럼 값이 지저분하게 저장되게 됩니다.

• 따라서 값을 깔끔하게, 저장하고 싶을 경우에는 다음처럼 처음부터 floating point로 사용하시는 것이 아니라, 분모, 분자를 모두 decimal.Decimal()로 넘겨서 사용하시는 것이 좋습니다.

print(decimal.Decimal(0.1))
print(decimal.Decimal(1)/decimal.Decimal(10))

0.1000000000000000055511151231257827021181583404541015625
0.1

control precision in Decimal

• decimal.getcontext().prec를 통해 precision을 어디까지 고려할 것인지를 조절할 수 있습니다.

import decimal 
decimal.getcontext().prec = 6
print(decimal.Decimal(1)/decimal.Decimal(7))
decimal.getcontext().prec = 20
print(decimal.Decimal(1)/decimal.Decimal(7))

0.142857
0.14285714285714285714

compute PI with Decimal

• 자 이제 decimal을 이용해서 pi를 제대로 계산해봅시다.
• 기존에서는 floating point를 50개까지밖에 고려하지 못했어요.

## pure python case 
def each_k(k):
    return 1/(16**k)*( 4/(8*k+1) - 2/(8*k+4) - 1/(8*k+5) - 1/(8*k+6))
pi_approximated = sum([each_k(i) for i in range(0, 50)])
print(f"{pi_approximated:.75f}")## 기본적으로는 소수점 50자리 정도까지만 계산됨 
## numpy case 
pi_approximated_np = np.array([each_k(i) for i in range(0, 50)], dtype=np.float128)
pi_approximated_np = pi_approximated_np.sum()
print(f"{pi_approximated_np:.75f}")

3.141592653589793115997963468544185161590576171875000000000000000000000000000
3.141592653589793115997963468544185161590576171875000000000000000000000000000

• 하지만 decimal을 이용하면, 다음처럼 더 복잡하게 계산할 수 있습니다.

## with decimal 
import decimal 

def each_k_with_decimal(k):
    ## interger를 모두 decimal.Decimal로 세팅하고 계산해줘야 문제가 없음 
    r = decimal.Decimal(1)/decimal.Decimal(16**k)
    r *= decimal.Decimal(4)/decimal.Decimal(8*k+1) - decimal.Decimal(2)/decimal.Decimal(8*k+4) - decimal.Decimal(1)/decimal.Decimal(8*k+5) - decimal.Decimal(1)/decimal.Decimal(8*k+6)
    return r
decimal.getcontext().prec = 200 ## precision 조절 
pi_approximated_decimal = sum([each_k_with_decimal(i) for i in range(0, 50)])
print(f"{pi_approximated_decimal:.205f}")

3.1415926535897932384626433832795028841971693993751058209749445922466544481906209319125159482533123956801188731427042180332333508312678923793809441272231338840779369704611268438173948214903863755033071000000

wrap-up

• 사실 저의 경우는 그렇게까지 floating point에 민감한 계산을 해본 적이 없습니다. 뉴럴넷을 돌리거나 할때도 뭐 그렇게까지 민감한 값을 돌릴 일들은 없으니까요.
• 다만, banker’s rounding은 좀 흥미로웠고, 정확히 알지 못했던 지점, 오차가 쌓이면 어떤 일이 발생하는지를 다시 알 수 있게 되었고, 컴퓨터가 숫자를 어떤 식으로 저장하고 관리하는지(특히 floating number에서 발생할 수 있는 오차들)를 명확하게 알게 되어서, 이후 매우 정밀한 계산을 해야 할때 참고할 수 있을 것 같습니다.
• 특히, 계산할 때 일종의 lazy evaluation처럼 abstract syntax tree형태로 값을 저장해두고, 필요할때 계산하면 훨씬 최적화되어 있는 계산을 할 수 있지 않을까? 하고 생각만, 해봅니다. 허허

reference

• pyconkr2017 - 보다 정확한 숫자 계산