networkx - equivalent lattice network.
3-line summary
- small-world network는 “높은 clustering”, “짧은 average shortest path lenght”를 가진다.
- 따라서, lattice network(highly clustered, long shorest path lenght)와 random network를 reference로 비교하여, 적합성을 판단한다.
- 본 포스트에서는, 그냥 greedy하게 clustering coefficient를 찾아가며 graph latticization하는 방법을 정리하였다.
what is lattice network(or graph)?
- lattice network or lattice graph는 아래 그림처럼, 격자(lattice)의 형태로 존재하는 네트워크를 말합니다. 이 격자는, 보통 “삼각형”을 많이 쓰지만, “사각형”, “육각형”도 많이 쓰이죠(육각형을 이용한 격자는 벌집이 있죠)
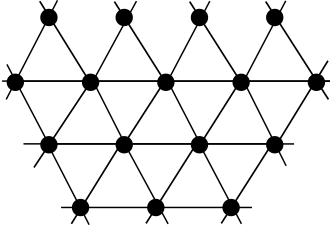
- 기본적으로는 보통 lattice network라고 하면, “triangular lattice network”를 말하게 됩니다. 그리고, 당연히 “삼각형의 수”를 기반으로 밀집도를 측정하는 clustering coefficient는 lattice graph에서 매우 높게 나오게 되죠. 그리고, 반대로, “average shortest path length”는 매우 높게 나오게 됩니다.
lattice network in small-worldness.
- small world network의 경우, “clustering coefficient는 높은데, average shortest path lengh는 짧다”라는 특성을 가집니다.
- 이 때, “clustering coefficient가 높다”라는 것을 참고하기 위해서, 이전에는 random network를 사용했지만, 보다 정확하게 측정하기 위해서 lattice network의 clustering coefficient를 사용할 수 있습니다. lattice network의 경우 굉장히 높은 clustering coefficient를 가지게 되니까요.
- 따라서, “equivalent lattice network”는 “기존 Random network와 degree가 동일하고, clustering coefficient가 매우 높은 network”라고 일단은 말씀드릴 수 있겠습니다.
greedy latticization
- 논문 The Ubiquity of Small-World Networks을 참고하면 latticiation 하는 방법에 대해서 나와 있습니다.
- 그리고, networkx - lattice reference에서도, “diagonal matrix까지의 거리를 이용하여 latticiation하는 방법”을 소개하고 있습니다.
- 하지만, 이 방법이 미묘하게 이해되지 않고(물론, 더 exact하고, 시간은 더 빨라 보입니다만), 앞서 말한 바와 같이 “clusteringg이 높고, 평균 최단 거리만 크면 되는거 아냐? 싶어서, 저는 그냥, greedy하게 clustering coefficient를 높여가는 식으로 진행했습니다. 논문 The Ubiquity of Small-World Networks에도 해당 내용에 대해서 다음과 같이 언급하고 있기도 하구요.
Storing the initial adjacency matrix and its clustering coefficient, the latticization procedure is performed on the matrix. If the clustering coefficient of the resulting matrix is lower, the initial matrix is kept and latticization is performed again on the same matrix; if the clustering coefficient is higher, then the initial adjacency matrix is replaced. This latticization process is repeated until clustering is maximized. This process results in a highly clustered network with long path length approximating a lattice topology.
- 따라서, 다음 챕터에서 python으로 구현해보았습니다.
greedy latticization with python
- connectedness를 유지하면서, edge를 교환한다는 점에서,
nx.lattice_reference와 진행방식이 동일합니다. - 다만, 하나의 조건이 더 들어가서, “교환 전의 edge exchange보다 clustering coef가 커질 때만, edge 를 교환”한다는 것이 다르죠.
- 원래의 greedy latticization과는 조금 다릅니다만, 오히려 이렇게 했을 때
nx.lattice_reference로 만들어지는 경우보다, clustering coefficient가 더 높고, average shortest path length가 더 낮게 나오곤 합니다.
python code
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
def lattice_reference_greedy(G, seed=None):
"""
`nx.lattice_reference`에서는 D라는 matrix를 바탕으로
diagonal matrix와의 거리를 측정하면서 진행하였으나, 몇가지 이해가 가지 않는 부분이 있어,
여기에서는 그냥 greed하게 처리함.
그냥, 'clustering coef'가 이전보다 커지면
그때 edge exchange를 진행하는 식으로 greedy하게 처리함.
"""
RandGen = np.random.RandomState(seed=seed)
G = G.copy()
nodes, degrees = zip(*G.degree()) # keys, degree
pdf_by_degree = [d / sum(degrees) for d in degrees]
(nnodes, nedges) = len(G), len(G.edges())
ntries = int(nnodes * nedges / (nnodes * (nnodes - 1) / 2))
edge_exchange_count = 0
max_clustering_coef = nx.average_clustering(G)
for i in range(0, nedges):
# edge exchange try.
for j in range(0, ntries):
#print(f"{i}, {j}")
# edge exchange를 할 수 없는 경우가 있으므로,
# ntries 만큼 시도하고, 없으면 그냥 넘어감.
# 우선 두 노드 a, b 를 고르고.
a, b, = RandGen.choice(nodes,
size=2,
p=pdf_by_degree,
replace=False)
# 두 노드 a, b의 이웃 노드를 고르고,
# new_b_nbr: uniform하게 선정된 a의 neighbor
# new_a_nbr: uniform하게 선정된 b의 neighbor
new_b_nbr = RandGen.choice(list(G[a]), size=1)[0]
new_a_nbr = RandGen.choice(list(G[b]), size=1)[0]
# a, b, c, d가 모두 다른지 체크하고
# 또한, 이미 연결되어 있는 것이 아닐때, edge exchange가 가능함.
if (a != new_a_nbr) and (b != new_b_nbr) and (new_b_nbr !=new_a_nbr):
if (new_a_nbr not in G[a]) and (new_b_nbr not in G[b]):
# ************************************************
# equivalent random network: 여기서 edge exchange
# equivalent lattice network:
# lattice network의 경우 clustering coef가 높음.
# 따라서, 여기서, clustering 값을 비교하여, 높게 해줄 경우, 변경.
# 공식적인 방식은 아니지만, 이렇게 해도 대충 됨.
# ************************************************
# 일단 바꾸고,
G.add_edge(a, new_a_nbr)
G.add_edge(b, new_b_nbr)
G.remove_edge(a, new_b_nbr)
G.remove_edge(b, new_a_nbr)
new_clustering_coef = nx.average_clustering(G)
# 변경한 G의 clustering coef가 더 큼.
if new_clustering_coef>=max_clustering_coef:
if nx.is_connected(G) is True:
# 더 크고, 연결성도 유지되므로, valid.
max_clustering_coef = new_clustering_coef
edge_exchange_count += 1
#print("== edge exchanged")
break
# clustering이 더 커지지 않거나,
# connectivity가 유지되지 않으므로, edge exchange에 실패함.
G.remove_edge(a, new_a_nbr),
G.remove_edge(b, new_b_nbr),
G.add_edge(a, new_b_nbr),
G.add_edge(b, new_a_nbr)
return G
############################################################
print("--" * 30)
N = 1000
G = nx.scale_free_graph(n=N, seed=0)
G = nx.Graph(G)
# greedy_latticeG: greedy하게 clustering coef를 높여 가며 만든 network.
# nx_latticeG: networkx.lattice_reference로 만든 clustering이 높은 network
greedy_latticeG = lattice_reference_greedy(G, seed=1)
nx_latticeG = nx.lattice_reference(G, seed=1)
# check connectedness
assert nx.is_connected(G)
assert nx.is_connected(greedy_latticeG)
assert nx.is_connected(nx_latticeG)
# check degree dict.
assert dict(nx.degree(G)) == dict(nx.degree(greedy_latticeG))
assert dict(nx.degree(G)) == dict(nx.degree(nx_latticeG))
# print average_clustering
print(f"clustering coef of G: {nx.average_clustering(G)}")
print(f"clustering coef of greedy lattice G: {nx.average_clustering(greedy_latticeG)}")
print(f"clustering coef of nx lattice G: {nx.average_clustering(nx_latticeG)}")
print("--"*30)
nx.average_shortest_path_length
# print average_clustering
print(f"avg shrt path l of G: {nx.average_shortest_path_length(G)}")
print(f"avg shrt path l of greedy lattice G: {nx.average_shortest_path_length(greedy_latticeG)}")
print(f"avg shrt path l of nx lattice G: {nx.average_shortest_path_length(nx_latticeG)}")
print("--" * 30)
# draw it.
def draw_networkx(G, file_name):
plt.figure()
nx.draw_networkx(G, pos=nx.spring_layout(G))
plt.savefig(file_name)
if True:
draw_networkx(G, "!G.png")
draw_networkx(greedy_latticeG, "!greedy_latticeG.png")
draw_networkx(nx_latticeG, "!nx_latticeG.png")
code output.
- 실행 결과는 다음과 같습니다.
nx.lattice_reference에 비해서, 제가 만든 greedy lattice가 clustering coefficient가 훨씬 높고, average shortest path length 도 큰 차이가 없는 것을 알 수 있습니다.
------------------------------------------------------------
clustering coef of G: 0.14510541684274386
clustering coef of greedy lattice G: 0.26693093604380685
clustering coef of nx lattice G: 0.14733398658864014
------------------------------------------------------------
avg shrt path l of G: 3.0883603603603604
avg shrt path l of greedy lattice G: 3.0983383383383383
avg shrt path l of nx lattice G: 3.106064064064064
------------------------------------------------------------
wrap-up
- 사실, 완벽한 lattice network는 아니죠. 다만, 제가 볼 때는 이렇게 해도 문제가 없을 것 같아요. 물론, 이것보다 더 빠르게 괜찮은 lattice network를 찾는 방법이 있겠죠.
- 다만, 동일한, degree sequence를 가질 때, 가장 clustering이 높은 graph는 반드시 latticiation이어야 하는지, 음, 그렇겠죠. 사실 그럴수밖에 없네요.
댓글남기기