networkx - strong connectivity and its condensation.

2-line summary

• node끼리 서로 양방향으로 path가 모두 있는 것이 strong-connectivity.
• 한 방향만 있는 것이 weak-connectivity.

strong connectivity

• https://en.wikipedia.org/wiki/Strongly_connected_component는 방향성이 있는 DiGraph, G에서 “각 partition 내에 서로 다른 node pair 간에 도달할 수 있는 양방향의 path가 모두 존재하는 것”을 말합니다.
• 반대로, 한 방향만 존재할 경우가 바로 weak connectivity죠.

strong-connectivity in networkx

• networkx - strong connectivity에는 다음의 함수들이 존재합니다.
  • nx.is_strongly_connected(DG): DG가 “강하게 연결되어 있는가?”
  • nx.number_strongly_connected_components(DG): DG에 존재하는 “강하게 연결되어 있는 Component들의 수”
  • nx.strongly_connected_components(DG): DG 내에 “강하게 연결된 component들을 리턴하는 generator”
• random하게 edge를 만들면서 추가하면서, DG의 strong-connectivity가 어떻게 변화하는지를 다음 코드를 통해 정리하였습니다.

import networkx as nx
import numpy as np

np.random.seed(0)

# random으로 edge를 추가해가면서, Component가 얼마나 생기는지를 확인함.
DG = nx.DiGraph()
N = 30
DG.add_nodes_from([i for i in range(0, N)])

MAX_E = len(DG) * (len(DG) - 1)
EACH_E = 20  # 한번에 업데이트되는 edge의 수, 즉 `EACH_E`만큼 새로운 Edge를 추가함.
for i in range(0, MAX_E // EACH_E):
    #============================================
    # INSERT Edge
    for _ in range(0, EACH_E):
        while True:
            u, v = np.random.randint(0, len(DG), 2)
            if v not in DG[u]:  # u, v not connected
                DG.add_edge(u, v)
                break
    #============================================
    print(f"== edge size: {len(DG.edges())}")
    print(f"== nx.is_strongly_connected(DG): {nx.is_strongly_connected(DG)}")
    #print(f"== nx.is_weakly_connected(DG)  : {nx.is_weakly_connected(DG)}")

    print(
        f"== nx.number_strongly_connected_components(DG): {nx.number_strongly_connected_components(DG)}"
    )
    #print(f"== nx.number_weakly_connected_components(DG)  : {nx.number_weakly_connected_components(DG)}")
    strong_comms = [strong_com for strong_com in nx.strongly_connected_components(DG)]
    strong_comms_size_lst = sorted([len(c) for c in strong_comms], reverse=True)
    print(f"== component size dist: {strong_comms_size_lst}")
    print("--"*30)
    if nx.is_strongly_connected(DG)==True:
        break
    #===========================================================================

• 뭐, 사실 weak connectivity와 비슷하게, 진행되죠.

== edge size: 20
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 30
== component size dist: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
------------------------------------------------------------
== edge size: 40
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 19
== component size dist: [12, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
------------------------------------------------------------
== edge size: 60
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 13
== component size dist: [18, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
------------------------------------------------------------
== edge size: 80
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 11
== component size dist: [20, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
------------------------------------------------------------
== edge size: 100
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 4
== component size dist: [27, 1, 1, 1]
------------------------------------------------------------
== edge size: 120
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 2
== component size dist: [29, 1]
------------------------------------------------------------
== edge size: 140
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 2
== component size dist: [29, 1]
------------------------------------------------------------
== edge size: 160
== nx.is_strongly_connected(DG): True
== nx.number_strongly_connected_components(DG): 1
== component size dist: [30]
------------------------------------------------------------

Condensation of a Graph.

• Condensation of Graph는 각 “Strong Connected Compnent”를 node로 변경하여 생성해내는 directed acyclic graph를 말합니다.
• 각 Strong Connected Component가 특정한 의미를 가진다면, 이를 Condenstaion하였을 때 생성되는 Graph 또한 새로운 의미를 가질 수 있겠죠.

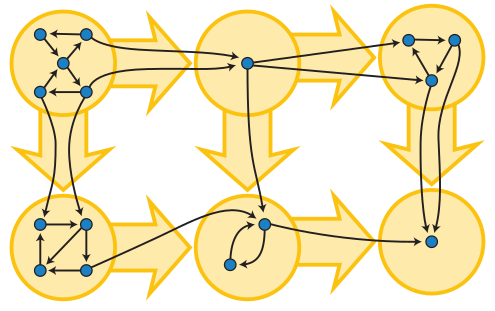
• 아래 코드에서는, 임의의 DG를 만들고, strongly connected component를 만든다음, 이를 condenstaion하여 새로운 G를 만들어봤습니다.

import networkx as nx
import numpy as np

np.random.seed(0)

# random으로 node를 만들어가면서 Component가 얼마나 생기는지를 확인함.

N = 30

# Directed Graph를 만들고
# edge에 weight를 uniform한 distribution으로 만듬.
DG = nx.DiGraph(nx.complete_graph(N))
edge_weight_dict = [(u, v) for u in DG for v in DG if u!=v]
edge_weight_dict = dict(zip(edge_weight_dict, np.random.random(N*(N-1))))
nx.set_edge_attributes(DG, edge_weight_dict, 'weight')

# edge_weight_threshold보다 작은 edge를 삭제하여
# strongly_connected_component의 수를 확인해봄

print("==" * 30)
edge_w_threshold = 0.92
print(f"edge_w_threshold: {edge_w_threshold}")
#print(DG.edges(data=True))
remove_edge = [(e[0], e[1]) for e in DG.edges(data=True) if e[2]['weight']<=edge_w_threshold]
DG.remove_edges_from(remove_edge)
print(f"== edge size: {len(DG.edges())}")
print(
    f"== nx.is_strongly_connected(DG): {nx.is_strongly_connected(DG)}")
print(
    f"== nx.number_strongly_connected_components(DG): {nx.number_strongly_connected_components(DG)}"
)
print("=="*30)

# nx.condesnation(DG)
# strongly_component를 node로, component간의 연결을 edge로 고려하여 변형한 G

condensed_DG = nx.condensation(DG)
print("== Condensed G")
print("== Nodes")
for n, n_attr in condensed_DG.nodes(data=True):
    print(f"{n} :: member of {n} => {n_attr['members']}")
print("==" * 30)

• 위 코드의 실행 결과는 다음과 같습니다.

============================================================
edge_w_threshold: 0.92
== edge size: 85
== nx.is_strongly_connected(DG): False
== nx.number_strongly_connected_components(DG): 5
============================================================
== Condensed G
== Nodes
0 :: member of 0 => {11}
1 :: member of 1 => {0, 1, 2, 3, 4, 5, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 23, 24, 25, 26, 27, 28}
2 :: member of 2 => {6}
3 :: member of 3 => {22}
4 :: member of 4 => {29}
============================================================

reference

• Strongly connected component
• Networkx - strong connectivity