frhyme

always doing another thing

데이터의 차원을 줄여봅시다.

4 분 소요

데이터 차원을 왜 줄여야 하나요?

  • 우선 쓸모가 없으니까요. 사람들이 빅데이터라는 말을 하기 시작한 이후부터는(물론 저 단어는 정말 쓸모없습니다만), 가령 엑셀같은 데이터에 그냥 칼럼이 엄청 많아도 너무너무 좋다고 생각할 지도 모릅니다. “우리에게는 빅데이터가 있어” 라고 생각할지도 모르죠. 그런데, 그 데이터의 대부분의 칼럼이 단 하나의 변화를 표현할 뿐이라면요? 계산 시간과 리소스는 많이 잡아먹지만, 별 필요가 없다면요? 그래도 괜찮을까요? 쓸모없는 데이터를 줄입시다. 필요업어요.
  • 데이터를 예쁘게 보고싶으니까요. 인간이 시각화된 데이터를 인지하는 차원은 아직은 3차원이 맥스입니다. x,y축 그리고 색. 3차원으로 렌더링을 하면 그림이 안 이쁘죠. 아무튼 그렇기 때문에 사람이 인지적으로 그림을 직관적으로 이해하려면 차원을 줄이는 것이 필요합니다.
  • 물론 말을 좀 대충하기는 했지만 dimensionality-reduction의 가장 중요한 목적은 숨겨진 데이터의 가장 간단하고 핵심적인 구조를 파악한다 라고 생각하면 좋습니다. 만약 차원을 줄이다가, 중요한 구조를 하나 잊어버린다거나 할 경우, 차원을 축소한 의미가 없으니까요.

PCA(Principal Component Analysis)

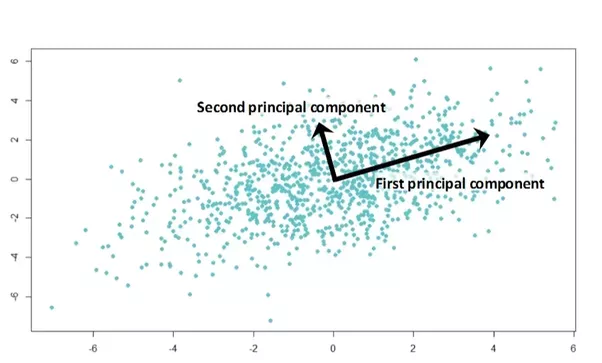
  • 한국말로 하면 ‘주성분분석’정도가 되려나요? t-SNE는 안 들어보셨어도 보통 PCA는 학부 과정에서 한 두번 정도 들어보셨을 것 같긴 합니다만, “전체 데이터 분포의 구조를 orthogonal한(서로 직교하는) linear한 vector의 합으로 표현하는 방식”이라고 생각하시면 될 것 같습니다.
  • 혓바닥이 기니까 일단 그림으로 설명하겠습니다. 그림에서 보시면 전체 데이터 분포를 보았을 때, first pricipal component만 봐도 대략적인 데이터의 경향성을 볼 수 있지 않을까요? 물론 second principal component도 매우 중요하지만, 첫번째가 현재 데이터의 분포를 더 잘 설명해주는 벡터인 것은 맞습니다. 그렇다면 만약, 이 2 차원의 데이터를 first principal component를 중심으로 한 1차원의 데이터로 줄여준다고 해도 어느 정도 괜찮을 것 같습니다(물론 ‘어느 정도’ 괜찮은지 도 매우 중요한 이슈입니다만).

pca example

  • PCA 가 가진 몇 가지 가정은 다음과 같습니다.
    • 데이터의 분포는 선형적인 벡터에 의해 설명된다: 예를 들어 달팽이 모양의 무엇이 있다면, 이는 PCA로 했을 경우 문제가 생깁니다.
      • 뒤쪽에서 할 mnist데이터에 대해서 PCA를 수행했을때 t-SNE만큼 잘 되지 않는 것은 mnist 데이터가 구불구불한 숫자들이기 때문이죠.
    • 전체 데이터 분포에서 큰 분산을 가지는 방향(first principal component)의 벡터가 가장 중요하다고 생각합니다.
    • 모든 벡터는 orthogonal하다
  • 뒤쪽의 방법들은 확률적인 분포를 고려한다. 그래서 방법 내부에 거리를 어떻게 측정할지 넘겨주는 argument가 있는데 PCA에서는 그런거 없다(음 생각해보니 당연하군)

t-SNE

  • t-SNE는 t-distributed Stochastic Neighbor Embedding의 약자라고 한다는데, 뭔지 잘 모르겠다…ㅠㅠ 그러므로 개념을 하나씩 잡아가야할 것 같은데

SNE: 고차원 공간에서의 유클리디안 거리를 데이터 포인트의 유사성을 표현하는 조건부 확률로 변환하는 방법

  • 이라고 합니다만, 이를 제 언어로 다시 표현하자면, 데이터간의 거리를 원래는 유클리디안 거리로 측정했다면, 데이터 간의 거리를 데이터의 분포를 고려하여 다시 표현했다고 할 수 있는 것 같습니다. 전에 Mahalanobis distance의 경우도 점들이 촘촘하게 있을 경우, 이를 고려하여 거리를 측정해야 한다고 했던 것처럼 SNE의 경우도 이렇게 다른 데이터 간의 분포를 고려하여 측정해야 한다고 하는 것이겠죠.
    • 여기서 “t”가 붙어있는 이유는 기존의 SNE에서는 gaussian distribution을 사용했는데 이보다 t-student distribution을 사용했더니 더 좋았기 때문이랍니다.
  • 음 왠지 이렇다면, 데이터가 n개 있을 때 n**2를 계산해줘야 하기 때문에 계산시간이 오래 걸릴 것 같습니다. 확인해보니, (200, 784)의 데이터를 (200, 2)로 축소할 때, PCA의 경우 0.28초 소요되는데 반면, t-SNE의 경우 5.39초 소요됩니다. n이 커지면 훨씬 더 많이 걸리겠죠.
  • 또한 뒤쪽 코드에서 보시면, 수행할 때마다 변환되는 형태가 다른 것을 알 수 있습니다(그림이 다름). 이렇게 일관적으로 해주지 못할 경우에는 feature extraction에 사용하는 것이 적합한지? 의문이 듭니다.

isomap??

k-neargest neighbor graph를 이용하여 다양체의 측지선 거리(geodesic distance: 그래프 상에서 두 점간의 가장 가까운 거리)를 구하고 다차원 척도 구성법을 이용하여 저차원 공간에 투영한다.

  • swiss roll의 경우처럼 다차원 공간에서 구불구불하게 데이터들이 존재하는 경우에, 이 데이터를 임의로 펴주는 것이 필요하다. 이를 펴주기 위해서 이를 k-neargest neighbor graph로 만들어주고(정확히는 모르겠지만, 아마 거리상 유독 가까운 몇 놈들만 직접 네트워크 상에서 연결되어 있다고 가정하는 것이 아닐까),
  • 이들간의 layout을 적절하게 짜주는 것이 아닐까? 싶다. 물론 좀 더 봐야겠지만,
    • 그래서 sklearn.manifold.isomap에는 neighbors_algorithm를 함께 넘겨줄 수 있다.

sammon mapping

고차원 공간에서의 거리와 투영된 2차원 공간에서의 거리를 최대한 가깝게 만드는 차원 감소 기법

  • 뭐 간단히 말하면 “차원을 줄여도 얘네는 여전히 비슷하게 멀어여”라고 표현할 수 있을 것 같다. 내가 직접 코딩을 하면 좋겠지만 sklearn에 없기 때문에 따로 하지 않았다 하하핫.

do it!!.

  • 원래 썰 풀기전에 일단 해봐야 하는데, 너무 늦었습니다. 아래 코드를 실행하면 밑의 그림이 나옵니다.
# import mnist data
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.datasets import fetch_mldata
mnist = fetch_mldata("MNIST original")
X = mnist.data / 255.0 # np.array (70000, 784)
y = mnist.target # np.array (70000,)

"""
data가 너무 많아서, 계산시간이 오래 걸려서 임의로 샘플링을 했다.
t-sne의 경우 n이 커지면 너무 오래 걸림. 네 저는 맥북에어로....이걸 하고 있어요ㅠㅠ
""" 
def sample_n(X, y, n):
    selected_rows = [int(70000/n*i) for i in range(0, n)]
    new_X = X[selected_rows]
    new_y = y[selected_rows]
    return new_X, new_y

"""
계산해서 그림을 그려주는 함수입니다.
"""
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.manifold import Isomap
def dim_reduction_and_draw(TSNE_or_PCA_or_Isomap, X, y, output_file):
    new_X = TSNE_or_PCA_or_Isomap(n_components=2).fit_transform(X)
    f = plt.figure()
    plt.scatter(new_X[:, 0], new_X[:, 1], c=y, alpha=0.7)
    plt.title(output_file)
    plt.axis('off')
    plt.legend()
    plt.show()
    plt.savefig("../../assets/images/markdown_img/"+output_file)

new_X, new_y = sample_n(X, y, 2000)
dim_reduction_and_draw(TSNE, new_X, new_y, "TSNE.svg")
dim_reduction_and_draw(PCA, new_X, new_y, "PCA.svg")
dim_reduction_and_draw(Isomap, new_X, new_y, "Isomap.svg")

TSNE 결과

tsne

PCA 결과

tsne

Isomap 결과

tsne

what is manifold learning?

  • 예민하십 분은 이미 아셨겠지만, 앞의 코드를 보시면, PCA의 경우 sklearn.decomposition에 있고, TSNE의 경우는 sklearn.manifold에 있는 것을 알 수 있습니다.
  • 해당 데이터의 분포가 다차원인 경우(여러 번 접혀 있는 경우) 차원 축소하기 위해서는 sklearn.manifold에 있는 메쏘드를 쓴다고 생각하시면 될 것 같습니다.

wrap-up

  • 당장 구글에만 검색을 해봐도, pca가 좋은지, t-sne가 좋은지에 대한 이슈들이 많습니다. 가장 큰 차이라면 PCA는 모든 벡터들이 linear 하다고 가정하고 시작한다는 점. 따라서 local structure가 무너질 수 있다는 점이 있습니다. 특히 다면체(manifold)의 경우에는 PCA를 사용하는 것이 적합하지 않죠.
  • 그래도, 소요되는 시간을 고려하면 PCA가 월등하긴 합니다. 또한 t-SNE의 경우는 매번 결과가 달라지기 때문에 이를 적용하는 것에 문제가 있을 수 있습니다(일종의 overfitting 문제랄까요).
  • 결과적으로, 그냥 `데이터가 알아서 잘해줄거야’라기보다, 어떤 method를 쓸지에 대해서는 제가 제일 잘 알아야 하는 것 같습니다.

reference

댓글남기기