python으로 마코브 체인 만들어 보기

마코브체인이란 무엇인가?

• 학부 시절(까마득한…어라 10년 전이네…) 그러니까 2008년에 확률시스템분석 이라는 과목에서 마코브 체인을 처음 배웠습니다. 왠지 지금 다시 돌아가면 잘할 수 있을 것 같다는 쓸모없는 용기가 샘솟는 것을 보면 역시 인간은 망각의 동물.
• 아무튼, 마코브 체인은 글보다는 그림으로 설명하는 것이 더 이해하기 좋습니다.
  • 아래 그림에서 보는 것처럼, 우리가 보고 싶은 것, 여기서는 ‘날씨’가 되겠죠.
  • 여기서는 날씨를 세 가지의 명확한 state로 구분하였습니다.
    • Cloudy/ Rain/ Sunny
  • 또한 state to state probability 또한 정의됩니다.
    • Cloudy => Rain: 50%

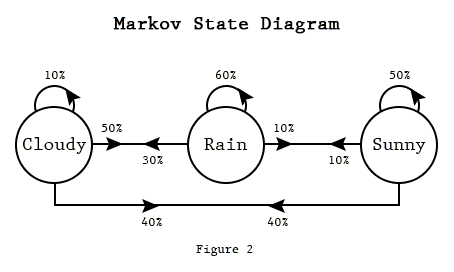
• 정리하면, 상황이 명확하게 구분되고(rain/cloudy/sunny) 상황에서 상황으로 변하는 확률이 명확하게 정의될 때, 이러한 마코브 체인을 쓸 수 있습니다. 마코브 체인을 배운 수업의 이름이 ‘확률시스템분석’이었는데, 지금 생각해보면, 아주 정확한 한글 번역이네요.

Markov Property

• “미래는 과거가 아닌, 현재의 상황에 의해서만 결정된다”라는 것으로, 이전에 어디 있었거나와 상관없이, 현재의 state에 의해서만 future state가 결정되는 성질. 일반적인 마코브체인은 A) cloudy => rain, B) sunny => rain 상관없이, 현재는 A,B 모두 rain이므로, A, B의 미래 state는 같은 확률로 결정된다.
• 물론, 이를 무시한, Markov chain with memory라는 것도 있습니다.

finite or infinite state

• 어떤 상황을 Markov Chain을 이용하여 모델링할 때, 우선 필요한 것은, 개별 상태(state)를 모델링하는 것입니다. 상태를 모델링하는 방법은 다양한데, 한정적(finite)일 수도 있고, 무한(infinite)일 수도 있습니다.
  • finite: 맑음/흐림/비옴, 기분 좋음/나쁨
  • inifite: birth/death 프로세스에서 현재 사람의 수가 state가 될 경우.
• 저는 이건, 모델링의 차이라고 생각합니다. 같은 대상이라도 경우에 따라서 서로 다르게 모델링할 수 있으니까요. 예를 들어 야구를 마코브 체인으로 모델링할 경우에
  • finite MC의 state: 아웃카운트/주자 상황 별로 상태를 24가지로 구분하여 모델링
  • infinite MC의 state: 득점/실점으로 상태를 모델링(개념상 득 실점 상황은 무한정)

Discrete or Continuous time

• Discrete time: 일반적인 MC는 모두 여기에 속하는데, time은 n, n+1와 같은 discrete space에 위치한다. 스텝이 하루/한 턴 등으로 고정되어 있다. t_1, t_2, ... , t_n이 모두 일관적인 차이로 구분됨.
• Continuous time: 상황이 정확하게 어떤 주기(discrete time의 경우 하루)를 중심으로 업데이트되면 좋겠지만, 사실 그렇지 않다.이보다는 어떠한 time interval로 구분된다고 보는 것이 실제 상황을 더 잘 모델링하는 방법이 됨. 따라서 이 경우에는 t_1, ... , t_n의 간격이 다를 수 있다는 것을 가정한다. 또한 이전 t_n부터의 간격 h의 크기에 따라, p값 또한 변화함
  • 요건, 좀 정리를 더 해봐야할 듯. 아직 나도 명확하지 못함.

do Example by python

• 저는 일단 파이썬으로 만들어 보면서 해보는 편이라, 파이썬으로 좀 만들어서 돌려보겠습니다.

DTMC: bull/bear/stagnant market

• 영문 위키의 예시를 그대로 따랐습니다. 증권 시장은 주별로 bull(강세시장)/bear(약세시장)/stagnant(침체시장) market 등으로 구분되는데, 매주 다음과 같은 state diagram 에 의해 변환된다고 할 수 있다고 합니다.
  • 이렇게 state diagram을 그린다는 것이 결국 markov chain으로 만들었다는 말이 됩니다.
  • 이렇게 보면, directed graph와 유사해 보이는 것을 알 수 있습니다.

• 해당 state diagram을 matrix로 만들고, matrix를 연속해서 행렬곱해주면, 현재의 상태에서 discrete step n 이후에는 어디에 있을 확률이 높은지를 예측할 수 있습니다. 이를 간단히 코드로 만들었습니다.

import numpy as np
p = np.array(
    [0.9, 0.075, 0.025, 0.15, 0.8, 0.05, 0.25, 0.25, 0.5]
).reshape(3, 3)
for i in range(0, 100):
    p = a.dot(p)
print(p)

• 간단하게 100번만 곱했는데, 수렴하는 것을 알 수 있습니다. 각각의 state는 순서대로, bull/bear/stagnant 이며, 일반적으로 bull market에 머무를 가능성이 0.625 정도 된다, 라고 말할 수 있습니다.

[[ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]
 [ 0.625   0.3125  0.0625]]

wrap-up

• 사실 markov chain을 더 정확하게 이해하려면 다음의 것들이 더 필요합니다만, 저는 더 정리하지 않았습니다.
  • irreducible markov chain
  • recurrent markov chain
  • aperiodic markov chain
  • ergodic
  • stationary distribution
• 저는 야구를 더 재밌게 공부하려고 하다보니까, 마코브체인을 다시 복습하기 위해서 본 것입니다. CTMC나 다른 것들을 보려고 하면 너무 힘이 들것 같아서, 저는 멈춥니다 하하핫. 다음에 필요하면 위의 부분을 정리할게요 하하핫.

reference

• https://www.datacamp.com/community/tutorials/markov-chains-python-tutorial
• https://en.wikipedia.org/wiki/Markov_chain