PaperSummary - Multi-scale structure and topological anomaly detection via a new network statistic - The onion decomposition

2-line summary

• k-core decomposition을 개선한 onion-spectrum을 제시하였다.
• 이는 k-core를 고려하되, “가장 작은 degree를 가지는 node를 순차적으로 잘라나가면서 서로 다른 layer에 배치하는 알고리즘”이다.

Multi-scale structure and topological anomaly detection via a new network statistic: The onion decomposition

• Nature scientific report에 2016년에 게재된 논문입니다.
• 해당 논문은 여기에서 볼 수 있습니다.

Abstract 번역

• 본 논문에서는, 네트워크의 구조적인 성질(structural property)를 다양한 층위에서(micro, meso, macro) 관찰할 수 있는 네트워크 지표를 제시하였다.
• 본 논문에서 제시한 지표인 “onion spectrum”은 onion decomposition에 기초하는데, 이는 기존에 있었던 k-core decomposition(표준적인 network fingerprinting)을 개선한 것이다. onion spectrum은 k-core처럼 쉽고 정확하게 계산해낼 수 있다.
• 그러함에도, onion spectrum은 네트워크에 대해서 더 풍성한 정보를 제공하는데, 가령, node heterogenetiy, degree correlation, centrality, tree or lattice-likeness 와 같은 정보들을 제공한다.
• 게다가, k-core decomposition과는 다르게, 혼합된 degree-onion spectrum은 “기존의 네트워크 조직과 특별히 다른 종류의 위상구조(topological structure)를 가지는 흥미로운 subgraph들을 발견할 수 있다.
• 본 논문에서는, onion spectrum을 실제 네트워크들과 표준적인 그래프 모델에 적용하여, 그 유용성을 증명했다.

other things.

onion-decomposition의 필요성.

• 비록, 이미 많은 지표들이 있다고 해도, multi-scale metric에 대한 필요성은 여전히 존재한다.
• 예를 들어, degree distribution과 local clustering은 매우 간단하고 동시에 많은 정보들을 담고 있지만, microscopic한 관점, 즉 network에 대한 지역적인 특성만을 담고 있다.
• Modularity나, 다른 community structure에 대한 성질들은 네트워크에 대한 meso-scale을 담고 있지만, 여전히 조악한(ill-defined) 부분이 있으며, network community에 대한 공통적인 정의는 아직 증명되지 못했따.
• 거시적인 관점(macroscopic)에서 betweenness centrality, eigenvector centrality, shortest path length의 경우, 전체 네트워크에 대해서 주어진 node의 역할을 특성화한다. 하지만, 여기에는 매우 높은 “계산 비용(computational effort)”이 발생하며, local understanding에 대해서는 거의 도움이 되지 못한다.

• 따라서, 미시, 거시 관점등 다양한 관점에서 network의 특성을 바라볼 수 있는 새로운 지표와 도구의 필요성이 대두된다.

• k-core decomposition을 개선한 알고리즘을 제시하였으며, 이를 통해, 특별한 subgraph들을 찾는 것에 성공했다. 본 연구에서는 undirected and unweighted network에 대해서 적용하였지만, 이훼 확장될 수 있을 것으로 본다.

k-core decomposition

• k-core decomposition은 k를 증가시키면서, k-core에 속하지 않는(k-crust)를 구분하면서 graph를 decomposition하는 것을 말합니다.
  • k-core는 “모든 노드가 최소한 k이상의 degree를 가지는 maximal-sub-network를 말하죠.
  • k-shell은 “정확하게 모든 node가 k의 degree를 가지는 것을 말합니다.
  • k-crust는 그래프에서 k-core를 빼고 남은 것들을 말하죠.
• 따라서, “낮은 값의 k-shell”은 보통 “중심부가 아닐 수 있습니다(less central)”, k가 높아질수록, 좀더 central core에 근접하게 되죠.

onion decomposition

• 언뜻 보기에는 onion decomposition 또한, k-core decomposition과 유사하게 보일 수 있습니다.
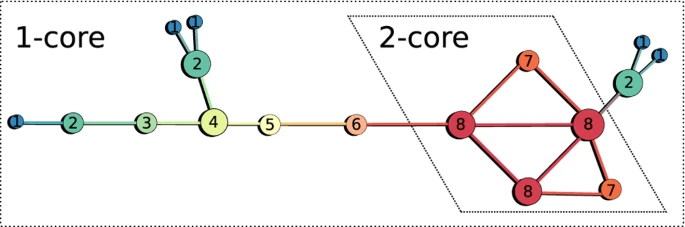
• 차이는, k-core가 아닌 것들을 다 잘라낸다는 것이 아니며, 외곽에 있는 node들을 순차적으로 잘라낸다는 것이 다릅니다. 가령, 1-shell이라도, 먼저 잘라지는 아이들과, 나중에 잘라지는 아이들이 다릅니다. 이를 구분하여, 각 layer에 배치했다는 것이 onion-decomposition이죠.
• 아래 그림을 보면 명확한데요. 사실 k-shell decomposition이라면, 아래 그림에서는 딱 2가지로 구분됩니다.
• 하지만, 1-core에서도, degree가 1개인 아이들과, degree가 1개 이상인 아이들이 존재하죠. 따라서, 이 차이를 두기 위해서, degree가 작은 아이들을 잘라나가면서, 각 아이들을 layer에 배치합니다.
• 조금 더 자세하게 설명하기 위해 예를 들어보자면 1) (isolate가 없다고 가정하고) 맨 처음의 graph G는 1-core죠(모든 노드가 최소 1의 degree를 가지니까요) 2) 현재 core가 1이므로, degree가 core인 1과 같거나 작은 모든 node를 잘라냅니다. 그리고 이 때 잘려나간 아이들이 첫번째 layer가 되겠죠 3) 가장 작은 degree를 가진 애들을 잘라냈지만, 여전히 1-core입니다. 다시, 또 잘라내고 이 아이들을 두번째 layer에 배치시킵니다. 4) 이를 반복하다 보니, 어느새 G가 2-core가 되었다고 합시다. 이때부터는, degree가 2와 같거나 작은 아이들을 잘라서 layer에 배치합니다. 5) 또 반복하다보니, G가 3-core라고 합시다. 그럼 이제, degree가 3과 같거나 작은 아이들을 잘라서 새로운 layer에 배치합니다. 6) 더이상 G에 node가 없다면, 이를 그만둡니다.
• 대략 이렇습니다. 즉, 원래라면, 그냥 k-crust로 묶여서 나갈 아이들이 사실은, 그 사이에도 계층적인 구조가 있다, 라는 것을 보여준 셈이죠.

wrap-up

• onion decomposition을 보다 보니, “그냥 degree가 제일 작은 node들을 매번 잘라내면서 layer를 쌓음”도 가능하지 않나 싶습니다만, 아마도 가장 높은 layer 내의 node들이 합쳐지지 않고, 너무 산발적이 될 것 같은 생각은 드네요.
• 즉, 그냥 min-degree decomposition과 k-core-decomposition의 사이에 이 decomposition이 있다는 생각이 듭니다.
• 또한, 이 알고리즘은 비교적 간단한 알고리즘으로 보이는데, 이렇게 해도 논문화가 되는군요(물론 validation을 훨씬 빡세게 처리하지 않았을까 싶습니다만).

reference

• Multi-scale structure and topological anomaly detection via a new network statistic: The onion decomposition
• networkx.algorithms.core.onion_layers