List 내 모든 역순(inversion) 수 찾기

List 내 Inversion 개수 찾기

• Array 혹은 List가 있을 때, 현재의 상태를 Sorted와 비교하여 얼마나 차이가 있는지 확인하려면, 현재 순서가 반대로 되어 있는 pair들이 얼마나 있는지 확인하면 되겠죠. 이렇게 역순으로 되어 있는 경우를 inversion이라고 합니다.
• 만약 sorted되어 있으면 inversion 값은 0이고, reversed sorted이면 inversion이 Array의 길이만큼 있겠죠.

Count Inversion with BubbleSort

• 가장 간단하지만, 가장 비효율적인 알고리즘은 BubbleSort를 이용하면 됩니다.
• 그냥 존재하는 모든 pair를 검색하고 Inversion인지 확인해서 +1을 해주면 되죠.
• Computation Time은 O(n^2)이지만, 추가로 필요로 하는 memory는 없죠.

lst = [...]
inversionCount = 0

for i in range(0, len(lst) - 1): 
    for j in range(i+1, len(lst)):
        if (lst[i] < lst[j]>):
            print("not Inversion")
        else:
            print("Inversion")
            inversionCount += 1

Count Inversion with MergeSort

• 사실 MergeSort를 거의 그대로 쓰면서 inversion이 몇 번 발생했는지를 더 쉽게 확인할 수 있습니다.
• mergeSort는 정렬된 왼쪽 Array와 정렬된 오른쪽 Array를 합쳐가면서 정렬하는 알고리즘이죠.
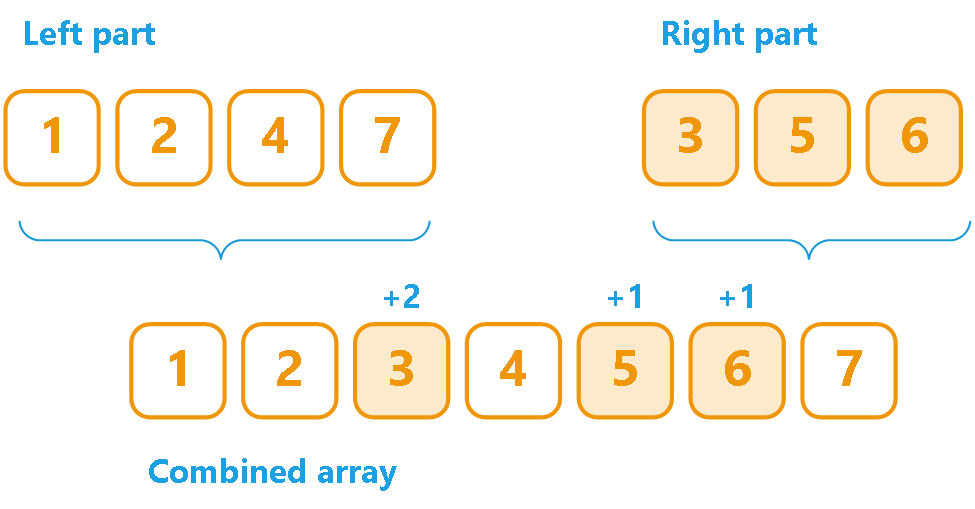
• 아래와 같은 그림에서 보면, 좀더 명확하죠.
  • leftSubArray, rightSubArray는 정렬되어 있다.
  • leftSubArray의 모든 원소는 rightSubArray의 모든 원소들보다 이전에 있다.
  • 따라서, 만약 leftSubArray의 i번째 원소가 rightSubArray의 j번째 원소보다 크다면, i번째 원소 뒤에 있는 모든 원소들을 당연히 j번째 원소보다 큰 것이다.
  • 따라서, leftSubArray의 i번째 원소 뒤 쪽으로는 모두 inversion이 발생한 것이다, 라고 할 수 있는 것이죠.

• 즉, 사실 mergeSort와 다른게 하나도 없습니다. merge할 때, 왼쪽 어레이의 i번째 원소 값이 오른쪽 어레이의 j번째 원소보다 큰 경우가 발생하면, “아 그럼 i번째 뒤의 원소들은 모두 j번째 원소보다 크겠네”라는 결론이 나는 것이죠.

python Implementation

• 이를 코드로 구현하면 다음과 같습니다.

def mergeSort(rawArr, sortedArr, left, right):
    """
    > 왼쪽부터 bottom up으로 merge해 나가는 함수
    """
    inv_count = 0
    if left < right: 
        mid = (left + right) // 2
        inv_count += mergeSort(rawArr, sortedArr, left, mid)
        inv_count += mergeSort(rawArr, sortedArr, mid + 1, right)
        inv_count += merge(rawArr, sortedArr, left, mid, right)
    return inv_count

def merge(rawArr, sortedArr, left, mid, right):
    """
    > rawArr[left: mid]를 leftSubArray로 두고 
    > rawArr[mid+1: right]를 rightSubArray로 두고
    두 어레이를 merger하는데, 그 과정에서 inversion도 함께 확인한다.
    """
    i = left # leftSubArray의 인덱스
    j = mid + 1 # rightSubArray의 인덱스
    sorted_i = left # sortedArr의 인덱스
    inv_count = 0 # inversion Count

    # i가 left subArray의 구간을 넘지 않는지
    # j가 right subArray의 구간을 넘지 않는지 체크합니다.
    while (i <= mid) and (j <= right):
        if rawArr[i] <= rawArr[j]:
            # 왼쪽 요소가 오른쪽 요소보다 작습니다.
            # 즉, inversion이 아닌 상황이므로 inv_count를 증가시킬 필요가 없죠.
            sortedArr[sorted_i] = rawArr[i]
            i += 1
        elif rawArr[i] > rawArr[j]: 
            # 왼쪽 요소가 오른쪽 요소보다 큽니다.
            # 보통, mergeSort에서 swap이 발생하는 상황이죠. 
            # 그런데, mergeSort에서는 왼쪽 subArray와 오른쪽 subArray가 모두 정렬되어 있는 상황입니다.
            # 따라서, leftSubArray[i:]의 모든 원소들은 당연히 rightSubArray[j]보다 크겠죠. 
            # 즉, leftSubArray[i:]의 수만큼 inversion이 발생한 것이라고 말할 수 있습니다.
            sortedArr[sorted_i] = rawArr[j]
            inv_count += (mid - i + 1)
            j += 1
        else: # 이 경우는 존재하지 않음.
            print("Impossible Case")
        sorted_i += 1

    # 남아있는 왼쪽 어레이를 sortedArr에 넣어주고
    while i <= mid:
        sortedArr[sorted_i] = rawArr[i]
        sorted_i += 1
        i += 1
    # 남아있는 오른쪽 어레이를 sortedArr에 넣어준다.
    while j <= right:
        sortedArr[sorted_i] = rawArr[j]
        sorted_i += 1
        j += 1
    # 그리고, 정렬된 애들을 sortedArr에도 그대로 넣어주면 되죠.
    for loop_var in range(left, right + 1):
        rawArr[loop_var] = sortedArr[loop_var]
    return inv_count

• 간단하게 다음처럼 테스트를 돌봤습니다.

testArrays = [
    [1, 2, 3], 
    [3, 2, 1],
    [1, 4, 2, 3, 5]
]
for testArr in testArrays:
    result = mergeSort(testArr, [0] * len(testArr), 0, len(testArr) - 1)
    print("Inversion Count", result)

Inversion Count 0
Inversion Count 3
Inversion Count 2

Wrap-up

• 이해하고 나니까 참 쉽지만, 이해하기 쉽지 않았습니다 으흐흐흑.

Reference

• GeeksForGeeks - counting inversion